První část - maturitní úlohy
Maturitní zkouška na gymnáziu v Hradci Králové 1869
Z tohoto roku se dochovalo zadání opravného maturitního testu z matematiky, které bylo studentům předloženo v sobotu 12. června a bylo řešeno od 9 do 12 hodin dopoledne.
1. Rozřeš rovnici: $$ 3\sqrt{x}-7 =-4\sqrt{y} $$ $$ 5\sqrt{x}+3\sqrt{y}=8 $$
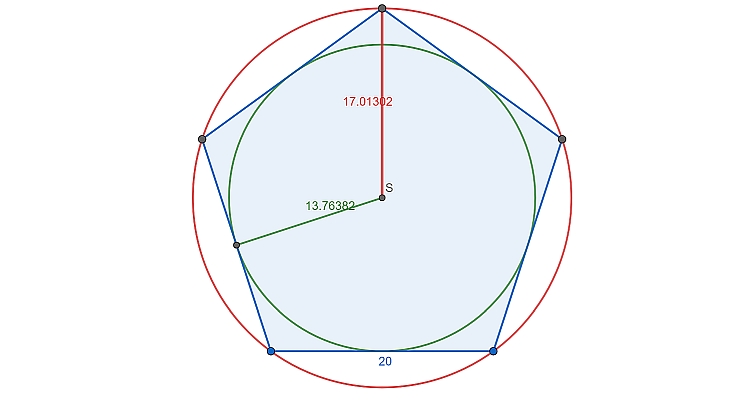
2. Strana pravidelného pětiuhelníku = 20“(20 palců). Vypočítej logarithmicky poloměr vepsaného a opsaného kruhu.
3. Rovnice $$ x^2 + y^2 = 100 $$ křivky (jaké má se určiti) a rovnice přímky: $$ 4y = x + 40 $$ jsou dány. Kolik bodů společných mají?
Řešení
1. $$ 3\sqrt{x}-7 =-4\sqrt{y} $$ $$ 5\sqrt{x}+3\sqrt{y}=8 $$
$$ 3\sqrt{x}+4\sqrt{y}=7 / x +3$$
$$ 5\sqrt{x}+3\sqrt{y}=8 / x -4$$
$$ 9\sqrt{x}+12\sqrt{y}=21 $$
$$ -20\sqrt{x}-12\sqrt{y}=-32 $$ Rovnice sečteme.
$$ -11\sqrt{x}=-11$$
$$ \sqrt{x}=1$$
$$ 3\sqrt{1}-7 =-4\sqrt{y} $$
$$ \sqrt{y}=1 $$
Řešení $$ x= y=1 $$
2. U této úlohy nevíme, jaké tabulky nebo připravené vzorce měli studenti k dispozici. Budu předpokládat, že měli k ruce následující vzorce pro výpočet poloměrů kružnice opsané a kružnice vepsané pravidelného pětiúhelníku a logaritmické tabulky. Pod pojmem Logaritmické tabulky se mohou skrývat Matematické tabulky např. i s tabulkami druhých odmocni, což mi připadá schůdnější, neboť ve vzorci je součet.
Vzorce: a je velikost strany pětiúhelníka
poloměr kružnice opsané $$r_o=\frac{1}{10} ( \sqrt{50+10\sqrt{5}} )a $$
poloměr kružnice vepsané$$r_v=\frac{1}{10} ( \sqrt{25+10\sqrt{5}} ) a $$
Poněvadž je strana pětiúhelníka 20 jedná se o použití Logaritmických tabulek pro výpočet odmocnin ve vzorcích. My použijeme kalkulačku, pak
poloměr kružnice opsané $$2\sqrt{50+10\sqrt{5}} = 17,01301616704079864363080994126 $$
poloměr kružnice vepsané$$2\sqrt{25+10\sqrt{5}} = 13,763819204711735382072095819109$$
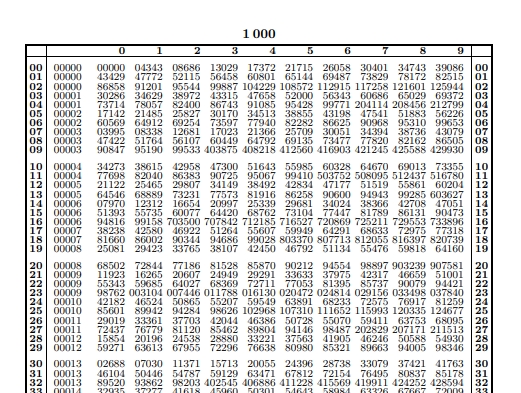
Ukázka logaritmických tabulek logaritmů o základu 10 (dekadické logaritmy) s přesností na 10 desetinných míst:
a co to zkontrolovat konstrukcí přes Geogebru
3. Jedná se o příklad na řešení soustavy rovnic lineární a kvadratické.
$$ x^2 + y^2 = 100 $$
$$ 4y = x + 40 $$
$$ (4y-40)^2+y^2=100$$
$$16y^2-320y+1600+y^2=100$$
$$17y^2-320y+1500=0$$
$$ D=(-320)^2-4*17*1500=102400-102000=400 $$ Tady by se asi mělo skončit, diskriminant je větší než nula, takže existují dvě řešení soustavy rovnic. Dopočteme:
$$ y_{1,2} =\frac{320 \pm 20}{34} $$
$$ x=4y-40$$
$$y_1 = 10 $$ $$x_1 = 0 $$
$$y_2 = \frac{150}{17} = 8,823... $$ $$x_2=4\frac{150}{17}-40=-\frac{80}{17}=-4,705... $$
Odpověď: existují dva průsečíky přímky a kružnice o souřadnicích $$ ( 0, 10 ) a (-\frac{80}{17} ,\frac{150}{17}) $$
a trochu grafiky (grafické řešení)
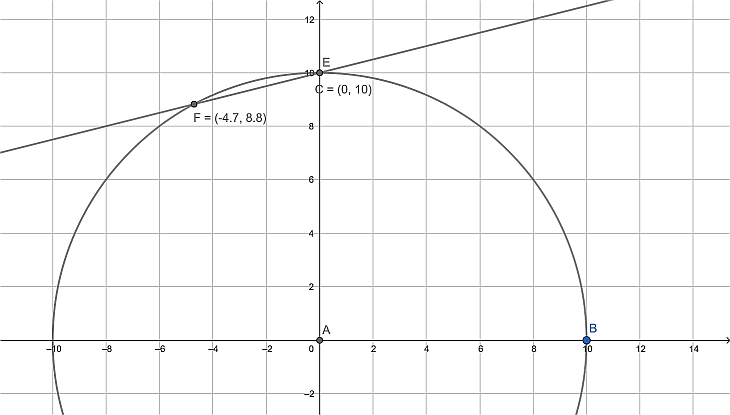
Něco navíc
Úloha 1
Určete velikost úhlu x.
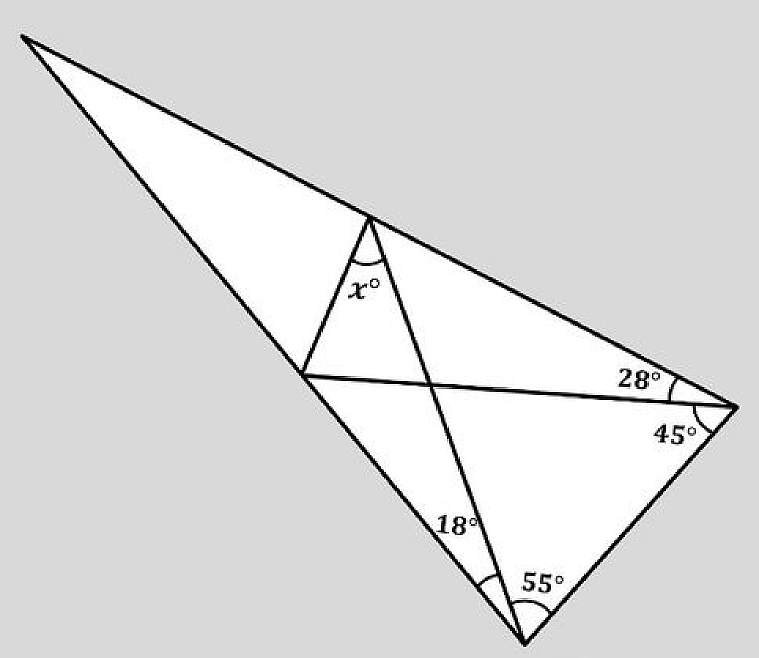
Řešení
Pokud přijdete na řešení bez pomoci goniometrie, tak dejte vědět. Goniometrické řešení uvádím ve článku Zajímavé úlohy
Výsledek je: x= 28,7057 stupně.
Úloha 2
Vypočtěte bez kalkulačky - jedná se o jednu z testových otázek pro přijetí do Oxfordu:
$$ log_2(3)= ?$$
Zaškrtněte správnou odpověď
A. mezi 1 1/3 a 1 1/2
B. mezi 1 1/2 a 1 2/3
C. mezi 1 2/3 a 2
D. mezi 2 a 3
Řešení
Využijeme vlastnost funkce logaritmus - je rostoucí ve svém definičním oboru.
Tedy pro $$x<y<z$$ platí $$log_2 x<log_2 y<log_2 z$$
Pak $$16 < 27 < 32 $$
$$log_2 2^4 <log_2 3^3 < log_2 2^5$$
Platí $$log_2 2 =1$$
Pak $$4 < 3log_2 3 <5$$
Tedy $$\frac{4}{3} <log_2 3 <\frac{5}{3}$$
$$1\frac{1}{3} <log_2 3 < 1\frac{2}{3}$$
Obdobně $$8 < 9 < 16 $$
$$log_2 2^3 <log_2 3^2 < log_2 2^4$$
Platí $$log_2 2 =1$$
Pak $$3 < 2log_2 3 <4$$
Tedy $$\frac{3}{2} <log_2 3 <2$$
$$1\frac{1}{2} <log_2 3 <2$$
A po průniku intervalů
$$1\frac{1}{2} <log_2 3 <1\frac{2}{3}$$
Odpověď B je správně. (Předpokládá se ovšem řešení zpaměti.)

