Maturita 1873 - písemná práce
1. Dvě místa A, B mají po dráze vzdálenost 30 mil. V prvém stojí cent uhlí 53 Kr., v druhém 85 Kr. Na kterém místě dráhy spojovací přišlo by uhlí z A tak draze, jako z B, kdyby stála doprava za cent a míli 3 Kr.?
2. Obsah kulové úseče jest v = 126.535, výška její h = 3.2. Jak velký jest poloměr koule, již tato úseč odpovídá?
3. Jak dlouhý jest onen průměr ellipsy, jejíž osy jsou 7´ a 4´ dlouhé, jenž uzavírá s delší osou úhel 20°36´.
Nebudu přepisovat řešení a okopíruji řešení z diplomové práce Veroniky Valáškové z roku 2016: Maturitní zkouška z matematiky do roku 1948.



A něco navíc
1. Zjednodušte \(\sqrt{17-\sqrt{240}}= ? \)
Tyto úlohy jsou standardní - pokud chceme odstranit vnější odmocninu, pak výraz pod touto odmocninou musí být druhá mocnina, takže zkusme
\( \sqrt{ (\sqrt{x}- \sqrt{y})^2}= \sqrt{ x+y- 2\sqrt{xy}}=\sqrt{ x+y- \sqrt{4xy}} =\sqrt{x}- \sqrt{y}\)
\( x+y=17 \) a \(4xy=240 \)
To lze řešit zpaměti (jinak to vede na jednoduchou kvadratickou rovnici)
\(x=12 \) a \(y=5\)
Pak
\(\sqrt{17-\sqrt{240}}= \sqrt{12}-\sqrt{5} \) ![]()
2. Určete obsah trojúhelníka
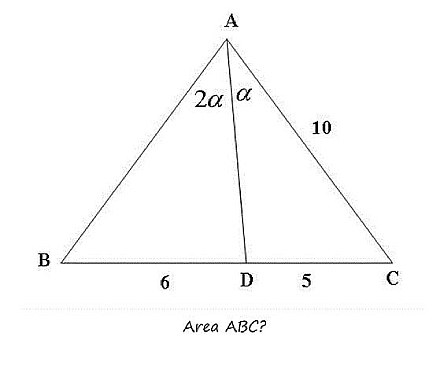
Řešení bez použití goniometrie vyžaduje znalost vět o ose úhlu v trojúhelníku:
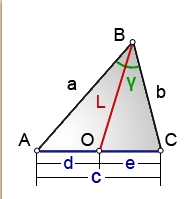
Platí \( \frac{a}{b} =\frac{d}{e} \)
a také
\( L^2=a\cdot b -d \cdot e \)
Pak povedeme bodem A osu uhlu \(\angle{BAD}\) a když si označíme průsečík na straně BC bodem E
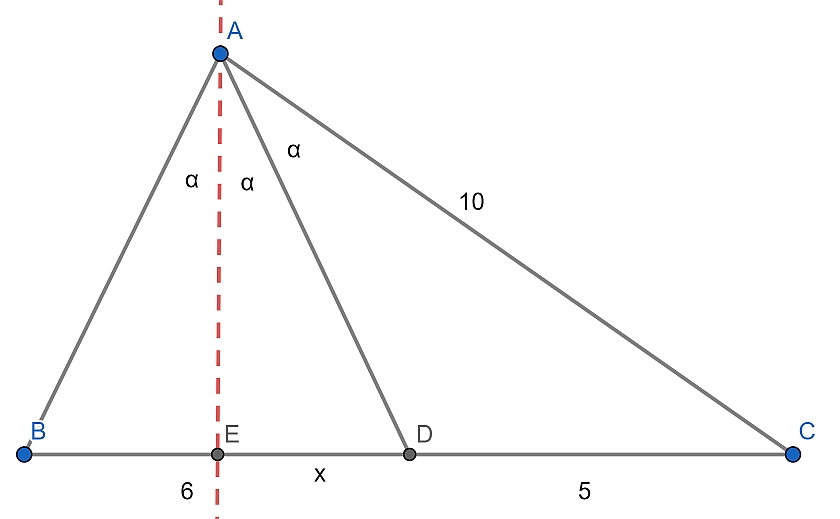
bude platit
\( \frac{AE}{10} =\frac{ED}{5} \) tj. \(AE=2\cdot ED \)
a ED označíme x
\( AE = 2x \)
a také
\( AD^2=10\cdot AE -5 \cdot x =15x\)
A nyní využijeme úhel \(\angle{BAD}\) a tedy
\(\frac{AB}{AD}=\frac{BE}{DE}\) tj. \(\frac{AB}{\sqrt{15x}}=\frac{6-x}{x} \)
tedy
\( AB \cdot AD =15\cdot (6-x) \)
a použijeme \( AE^2= AB\cdot AD - BE \cdot ED\)
\( AE^2= AB\cdot AD - BE \cdot ED\)
\( 4x^2= 90-15x-x(6-x)\)
tak
\( x^2+7x-30=0 \)
\( (x-3)(x+10)=0\)
\( x=3 \)
takže máme \( AE =6\) \(CE=8\) a \(AC=10\)
tedy trojúhelník AEC je pravoúhlý a tedy obsah \( S =\frac{BC\cdot AE}{2}=\frac{11\cdot 6}{2}=33\) ![]()

